为什么需要雪花算法:(背景)
随着业务的发展,数据库访问压力逐步增大,数据库的数据量也会增大。这个时候,我们就需要扩展数据库的性能,一般有以下三种方式:业务分库、主从复制(读写分离),数据库分表。正式由于数据库分表的需要,我们才需要雪花算法。
数据库分表
单表数据拆分有两种方式:垂直分表和水平分表。
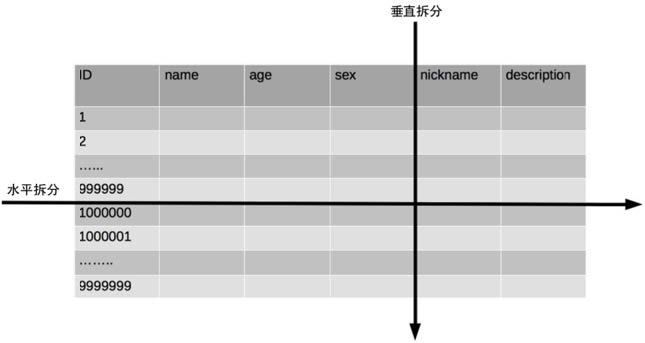
垂直分表
垂直分表适合将表中某些不常用且占了大量空间的列拆分出去。
例如,前面示意图中的 nickname 和 description 字段,假设我们是一个婚恋网站,用户在筛选其他用户的时候,主要是用 age 和 sex 两个字段进行查询,而 nickname 和 description 两个字段主要用于展示,一般不会在业务查询中用到。description 本身又比较长,因此我们可以将这两个字段独立到另外一张表中,这样在查询 age 和 sex 时,就能带来一定的性能提升。
水平分表
水平分表适合表行数特别大的表,有的公司要求单表行数超过 5000 万就必须进行分表,这个数字可以作为参考,但并不是绝对标准,关键还是要看表的访问性能。对于一些比较复杂的表,可能超过 1000万就要分表了;而对于一些简单的表,即使存储数据超过 1 亿行,也可以不分表。
但不管怎样,当看到表的数据量达到千万级别时,作为架构师就要警觉起来,因为这很可能是架构的性能瓶颈或者隐患。
水平分表两种方式
按照顺序分配

- 以最常见的用户 ID 为例,可以按照 1000万 的范围大小进行分段,1 ~ 1000万 放到表 1中,1000万零1 ~ 2000万放到表2中,以此类推。
- 优点是:可以随着数据的增加平滑地扩充新的表
- 缺点:如果表A存储万1000万条数据之后,我们再把数据放在表B,如果总的数据量只有1000万零2条,那么这样就会导致两张表的数据分布不均匀。导致表A的访问量过大,表B的访问量有太少,起不到分表的作用。
取模

- 同样以用户 ID 为例,假如我们一开始就规划了 3 个数据库表,可以简单地用 user_id % 3 的值来表示数据所属的数据库表编号,这样id=1的放在表A,id=2的放在表B,id=3的放在表C,以此类推
- 优点:表分布比较均匀。
- 缺点:扩充新的表很麻烦,所有数据都要重分布。如果每张表最大存储1000万条数据,3张表最多也只是存储3000万条数据。如果超过3000万条数据,我门又要用怎样的策略来存储数据呢?这就是一个难点。
有序主键和无序主键的区别(联想MySQL的存储结构)
有序主键(例如自增ID)
存储性能:好
- 插入数据:由于自增ID的连续性,新记录总是插入到索引的最后位置,符合B+树的增长方式。无需在中间位置插入或移动数据,因此插入过程简单,性能较高。
- 数据页分裂:因数据是顺序插入的,页分裂发生频率低。只有在数据页完全填满时才会新开数据页,以支持新的连续数据,避免了大量的数据重排和移动。
查询性能:
- 顺序插入的数据在物理上是连续存储的,因此基于主键的范围查询效率较高,减少了磁盘随机读写的次数。尤其是大范围查询时,数据连续分布在少数数据页中,可以减少IO操作。
无序主键(例如UUID)
存储性能:差
- 插入数据:UUID是随机生成的无序字符串,新插入数据无法确定插入位置,通常会插入到B+树的中间位置。每次插入都可能导致页分裂并重新组织索引,增加了数据重排的次数,导致存储开销更大。
- 数据页分裂:由于无序主键的随机性,数据插入分布不规律,页分裂频繁。当数据页满了时,系统会强制在中间位置插入新页,使得一部分记录被移动到新页。页分裂和数据移动会导致数据页利用率降低,影响插入性能
查询性能:差
- 数据分布在更多的非连续数据页中,影响了范围查询的效率。每次查询需要在多个不相邻的数据页中获取数据,磁盘的随机读写增加,导致查询性能下降。
主键自增的优缺点
优缺点
优点:
- 唯一性:每个记录的自增ID是唯一的,能够满足主键的唯一性要求。
- 顺序性:自增ID是连续递增的整数值,在插入时顺序排列,不会引起频繁的页分裂。
- 索引构建和维护成本低:因为自增ID按顺序增长,InnoDB在插入数据时无需频繁调整数据位置,索引维护成本较低,性能较高。
- 占用空间小:相比UUID等字符串类型的主键,自增ID通常是4字节或8字节整数,占用空间更少。
缺点:
- 存在业务数据泄露风险:连续的ID可能会让人推测出插入的总数量或增长规律,可能导致数据泄露风险。
- 跨库合并复杂:如果不同数据库或分片中使用相同自增ID策略,数据合并时容易**产生冲突**。
- 无法保证全局唯一:自增ID通常是数据库实例内部唯一,难以在分布式环境下保证全球唯一性。
主键自增可能产生id冲突问题
假设表A里面的数据删除了,那么就会有数据空余,
如果我们不管数据空余,放着,慢慢的删除的数据越来越多,就会操作数据分步不均匀
如果我们去填充数据,那么表A最后一条数据的Id就是1000零1(因为主键自增),就和B表的第一条数据冲突了
如果我们在填充数据之前,先去条件判断,如果发送冲突,就把冲突的数据改了,每次都这样的化,系统效率就很低
解决自增主键的影响
Hash/UUID
使用hash算法:特点无序且绝对重复
因为不重复,所以一定是不会有主键冲突的
可是因为hash/UUID是没有顺序的,所以会导致插入的时候效率低
聚簇索引:id如果有顺序查询效率高,id没有顺序查询效率低
雪花算法:有序且不重复
雪花算法是由Twitter公布的分布式主键生成算法,它能够保证不同表的主键的不重复性,以及相同表的主键的有序性。
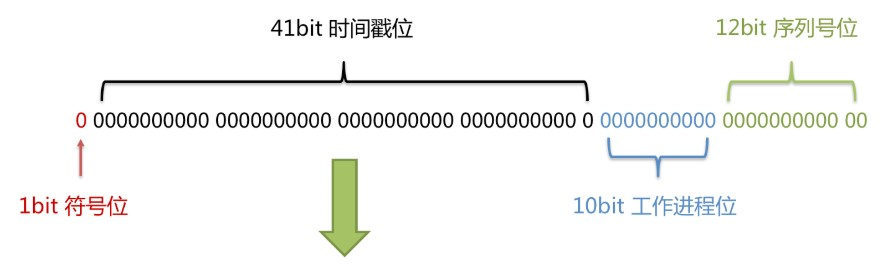
- 长度共64bit(一个long型)。
- 首先是一个符号位,1bit标识,由于long基本类型在Java中是带符号的,最高位是符号位,正数是0,负数是1,所以id一般是正数,最高位是0。
- 41bit时间截(毫秒级),存储的是时间截的差值(当前时间截 - 开始时间截),结果约等于69.73年。
- 10bit作为机器的ID(5个bit是数据中心,5个bit的机器ID,可以部署在1024个节点)。
- 12bit作为毫秒内的流水号(意味着每个节点在每毫秒可以产生 4096 个 ID)。
- 优点:整体上按照时间自增排序,并且整个分布式系统内不会产生ID碰撞,并且效率较高。
UUIDv7
基于时间排序:UUIDv7在设计上是时间顺序递增的,前42位编码了时间戳(以毫秒为单位)。在大多数场景下接近顺序增长,从而减少随机性带来的插入性能开销。
支持高并发环境:除了时间戳部分,UUIDv7还包含了一定的随机位和节点ID位,以保证在同一毫秒内生成的UUID不重复。且无需中心化的ID生成服务。
较好的查询和存储性能:因为UUIDv7有时间顺序特性,B+树结构的索引可以更高效地存储和查找UUIDv7,减少了数据页分裂的情况,提高了插入和范围查询性能。
长度和格式兼容:UUIDv7仍然保持UUID 128位长度和标准格式(8-4-4-4-12),这使得它可以直接替换掉传统的UUID版本而无需调整存储字段格式
总结
| 特性 | 自增ID | UUIDv4/Hash | UUIDv7/雪花算法 |
|---|---|---|---|
| 全局唯一性 | 无法保证 | 全局唯一 | 全局唯一 |
| 存储空间 | 较小(4-8字节) | 较大(16字节) | 较大(16字节) |
| 插入性能 | 高 | 较低(无序插入导致页分裂) | 较高(接近顺序插入) |
| 排序支持 | 支持顺序插入,查询高效 | 不支持,无序 | 支持,按时间顺序 |
| 可读性 | 较高 | 较低 | 较低 |
| 信息泄露 | 可能泄露插入顺序 | 隐藏插入顺序 | 基于时间顺序,部分暴露插入顺序 |
| 适用场景 | 单库系统,需要顺序性 | 分布式系统,只需唯一性 | 分布式系统需要顺序性和高插入性能 |
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1909773034@qq.com

